2. Se usa la función fft
con múltiplos de dos por ejemplo : 2, 4, 16, 32, 64,
128, 256, 512, 1024, etc.
3. La frecuencia de
adquisición de datos debe ser por lo menos el doble de
la frecuencia más alta en la señal.
4. Agregar ceros a la señal
no afecta a la transformada de Fourier pero si da más
resolución a la gráfica pero que pasa si agrego
una señal que no sea de la forma
sin(wt)+sin(wpt).
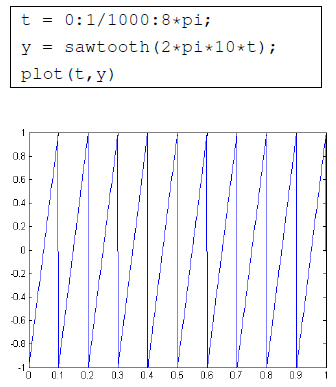
Apliquemos la transformada de Fourier a la
onda en forma de sierra con f = 10 Hz

Fíjate que la frecuencia fundamental
es el pico de mayor amplitud que es 10 Hz claro tiene sentido si
nuestra función tiene una f = 10 Hz , los otros picos
representan armónicos. Pero ¿qué son los
armónicos?
3.2 Sonido
La señal de sierra puede ser la
representación del sonido produce un violín. Si
tocamos otros instrumentos musicales la forma de la onda
sería diferente. Sin embargo el oído
escucharía la frecuencia fundamental de 10 hz más
los harmónicos como los dos instrumentos producen la misma
frecuencia fundamental para la misma nota deberán
escucharse casi igual y se dice tiene un "pitch" idéntico.
Como la amplitud de los armónicos es diferente el sonido
no es idéntico y se dice tienen diferente "timbre". A
pesar que el piano solo puede reproducir 20% de las frecuencia el
ser humano puede escuchar (4Khz a 20 Khz) puede producir
más del 70% de la información los humanos pueden
percibir ( 7 de 10 octavas ) en la vida real no podemos usar la
transformada de Fourier eficientemente ya que en su dominio
aparecen un montón de armónicos y frecuencia. En
ese caso podemos implementar filtros digitales y
análogos.
3.3 Serie de Fourier

Esta es la serie de Fourier. Resolvamos la
solución para la función de tipo sierra.

sustituyendo el valor de bn en la
ecuación (1)

como la funcion f(x) = x es impar el valor
de los coeficientes ""an"" es igual a cero. "L" representa el
periodo de la onda y ""A" es la amplitud. Ejemplo: Genera una
función tipo sierra usando la ecuación (6).
Amplitud = 5 y una frecuencia de 2 Hz y desarrolla los primeros
10 términos de la serie.
Fíjate que en matlab no podemos usar
esta técnica por las siguientes razones
• no tenemos un espacio ilimitado de
memo- ria para extender la serie hasta infinito
• las variables son
discretas
• no conocemos la función f(x)
represente nuestros datos
En la vida real solo trabajamos con datos
numéricos. En ocasiones es imposible generar una
interpolación y definir una función f(x). eso es la
realidad.
3.4 Interpolación
La idea de este método es generar un
polinomio de grado "n" para unir puntos en un patrón de
datos. Por ventaja matlab hace esto automaticamente. Teclea
"cftool" en el command window
• Para generara un polinomio de grado
"n" necesitas por lo menos "n" puntos en el plano
• cftool es la interfaz visual
facilita matlab para interpolación exponencial, Fourier,
polinomio, lineal , etc
Para iniciar la interpolación debes
exportar datos del workspace. Los siguientes datos son aleatorios
y se usaran para definir un ejemplo:
(1,4) (4,7) (9,11) (10,2) (11,8)
(15,3)
el primer digito corresponder a "x" y el
segundo digito a "y" (x,y)
Insertamos los datos en el command window.
un vector para los puntos en "x" y un vector para los puntos en
"y"
x = [ 1 4 9 10 11 15 ];
y = [4 7 11 2 8 3 ];
cftool
Graficamos. Matlab cuenta con muchas formas
de interpolar es este caso usaremos un polinomio de grado
"5"

Linear model Poly5:

Goodness of fit: SSE: 2.153e-022 R-square:
1 Adjusted R-square: NaN RMSE: NaN
Ahora sabes interpolar datos. Continuamos
con los usos y herramientas que ofrece Matlab
3.5 Transformada de
Laplace
Usada la mayor parte del tiempo en resolver
circuitos eléctricos. Por qué la usamos y su
función ? Laplace permite extendernos del dominio del
tiempo al dominio complejo "s". Otra manera definimos a la serie
de Fourier es en su forma compleja por

La ecuación (7) puede expanderse en
la transformada de Laplace, multiplicando la señal en el
tiempo por un término exponencial

para localisar valores en el plano complejo
se puede representar por letra s = s + iw y la ecuacion (9) se
puede escribir en una forma mas compacta

tambien existe la transformada inversa de
Laplace:

la ecuacion (11) es la forma formal de la
transformada de laplace pero no la usaremos. ya existe unas
tablas que facilitan ese trabajo.y lo mejor es que matlab puede
sacar la transformada de laplace. a continuacion se menciona un
ejemplo.
La tranformada de Laplace de la
funcion

Matlab contiene comandos muy simples. estos
son parte de un paquete "symbolic toolbox" para realizar los
siguiente ejemplos necesitas tener instalado el
paquete.
Encuentra la transformada inversa de
Laplace

la salida del codigo anterior es

Resuelve la siguiente ecuación
diferencial usando Laplace con las siguiente condiciones y(0)=2
y"(0)=2 y"(0)=0

el poder de Fourier radica su uso en
electrónica y diseño de filtros digitales. Los dos
tipos IIR ( infinite impulse response) y FIR ( finite impulse
response ). El filtro FIR se aplica usando un proceso llamado
convolucion (este término se asocia en este caso a proceso
digital de señales) mientras el IIR es aplicado mediante
Laplace y la transformada "z" eso es de esperarse. Recuerden un
decaimiento exponencial de la forma e-t tiende a cero en forma de
asíntota.

Resolvamos el circuito RCL anterior con la
ayuda de Laplace y encontremos su step re- sponse (función
de impulso ) y grafiquemos su resultado en Matlab.


La gráfica anterior muestra una
señal de entrada de corriente directa
Resolvamos usando la ley
conservación de la energía y dado que las
condiciones iniciales del sistema son cero.

Aplicando la transformada inversa de
Laplace a f(s) encontramos la step function en el dominio del
tiempo

ahora tenemos que graficar f(t) y observar
como el circuito se comporta en los primeros 6
segundos

Observamos el decaimiento exponencial. La
forma de un oscilador

Aunque la forma más compacta
representar la step fuction del circuito RCL anterior es por
medio de la ecuación (14) el uso de variables complejas
dificulta y hace casi imposible generar una gráfica la
solución es separar las parte real e imaginaria de la
variable "s". Los siguientes tips son útiles para saber en
qué se puede aplicar Laplace
1. La transformada de Laplace solo es
útil si se analizan funciones consisten de senos y
exponenciales
2. Filtros análogos se
diseñan usando la transformada de Laplace y recurisive
filtros mediante la transformada "z"
4 Ecuaciones
diferenciales ordinarias
Ahora entremos a métodos para
resolver dos tipos de ecuaciones diferenciales
ordinarias:
1. Ecuaciones diferenciales de segundo
orden con coeficientes constantes
2. Sistema de nxn ecuaciones diferenciales
de primer orden
Matlab cuenta con un paquete llamada "ODE
toolbox" en su siglas en ingles (ordinary differ- ential
equation) también cuenta con un paquete PDE ( partial
differential equation ) en este texto solo se mencionare el ODE y
en futuras ediciones se agregara el PDE. Para poder resolver una
ecuación diferencial en Matlab primero debe crearse un
M-file en otras palabras una función donde se introduce la
ecuación diferencial a resolver y deberá ser
invocada en el com- mand window insertando condiciones iniciales,
valores de tiempo , etc. La ecuaciones de un oscilador con
fricción se define por
myll + byl + ky = 0 (16)
La ecuación anterior es muy
fácil de resolver a mano pero será un buen ejemplo
para usar el ODE de Matlab.

haciendo la sustitución y"=y(2)
y=y(1) una ecuación diferencial de segundo orden puede
transformarse a una ecuación de 1er orden. Invoquemos la
m-file anterior tecleando en el command window lo
siguiente

Matlab regresa una matriz "y" de 2
columnas. Cada columna representa 1 de las 2 soluciones de la
ecuacions diferencial. Recuerda la solución de estas
ecuaciones diferenciales es una combinación línea
de la forma:
y(t) = C1Y1 + C2Y2 (17)
La gráfica del código
anterior con m =1 , b = .1 , k =1 y t de 0 a 40 segundos se
muestra a continuación.

Si cambiamos el valor de "b","m" y "k"
encontramos diferentes soluciones. Ahora editemos el m-file y sea
el coeficiente de fricción b = 1

Al aumentar la fricción el
decaimiento exponencial es mayor y la oscilación tiende a
cero más rápido. Si hacemos aun mayor el valor de
"b" no se observar oscilaciones en el sistema, sea b = 2 en el
siguiente ejemplo :

4.1 Introducción mecánica
clásica
La mecánica clásica ofrece un
sin número de problemas de sistemas de ecuaciones
diferenciales describiendo movimiento. El orden de la
ecuación diferencial correspondiente al movimiento del
sistema puede ser enorme. Aquí se tendrá en cuenta
lo siguiente para ayudar a reducir lo más posible el
número de ecuaciones
• Usar la energía
cinética y potencial para resolver el
movimiento
• No necesitas resolver para
aceleraciones
• Necesitas resolver velocidades
inerciales
La ecuación de Lagrange para
sistemas conservativos

en donde q es la coordenada generalizada y
los grados de libertad del sistema y "L" se define como el
lagrangiano y es la resta de la energía cinética y
potencial:

El método de Newton requiere que
encuentres todas las fuerzas de los sistemas en 3 direcciones y
reducir el problema. El método de Lagrange nos permite
reducir el problema resolviendo el número de ecuaciones y
usando algebra elemental.
• El lagrangiano requiere de saber
posición y velocidad del sistema
Otra manera de interpretar el movimiento es
mediante la mecánica de Hamilton la cual usa el momento y
posición para poder resolver el sistema. La energía
cinética debe estar en función del momento y no de
la velocidad.

Recuerda que esta es la energía
cinética en términos de física
clásica y no relativista El hamiltoniano es entonces la
transformación del lagrangiano y se define por la
transformación de Legendre:

Para cada velocidad hay un momento
generalizado

Así obtenemos las ecuaciones definen
al hamiltoniano

Apliquemos las anteriores ecuaciones al
péndulo doble

Encontremos el potencial y energía
cinética del sistema


Reducimos términos para el
potencial

Reducimos términos para la
energía cinética

Usando ecuación (19)

resolviendo entonces para

Resolviendo ahora para la siguiente
derivada parcial

Resolviendo para

La ecuación (35) y (36) son
ecuaciones diferenciales de segundo orden. Podemos usar la
transformación de Legendre y obtener el hamiltoniano.
Así obtener un sistema de 4 ecuaciones diferenciales de
primer orden y resolver usando el ODE de Matlab.

no daré todo el proceso paso a paso
como obtener el hamiltoniano porque estoy cansado de escribir en
latex y el álgebra es tediosa nota : por falta de espacio
se agrega C1 y C2 que tiene el siguiente valor

Después de obtener el lagrangiano y
resolver el álgebra ya podemos usar el siguiente
código y obtener la solución numérica:
recuerden la computadora solo es una maquina realiza un proceso
varias veces no puede obtener y generar ecuaciones por si
sola.
El siguiente código genera la matriz
de 4 ecuaciones diferenciales de primer orden, ver
ecuación (37)

Debemos salvar el código en formato
m-file e invocar la función. El siguiente código se
debe teclar en el command window sea m1 = 1 m2 = 1 l1 = 1 y l2 =
1 para el siguiente ejemplo (puedes variar las condiciones
iniciales, masas y longitud del péndulo:)

Invocando el primer ODE que se encuentra en
el código anterior

Invocando el segundo ODE que se encuentra
en el código anterior

Invocando el tercer ODE que se encuentra en
el código anterior invocando el segundo ODE que se
encuentra en el código anterior

Referencias
[1] Buerger, David J., LATEX for scientists
and engi- neers, (New York: McGraw-Hill, 1990).
http://www.wam.umd.edu/pe-
tersd/246/matlabode2.html
http://www.math.montana.edu/umsfj-
doc/dfieldtut.html
http://online.redwoods.cc.ca.us/instruct/darnold/
http://www.mathworks.com/
Autor:
Oscar Guerrero Miramontes
Ing. Física
México
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |